Entfernungsberechnung mit Quaternionen und Geodäten

Dies ist die HTML-Fassung des Preprints eines Artikels im Forschungsbericht 2011 der Hochschule Merseburg (FH). Die Inhalte dieser Fassung sind im Vergleich zum Preprint eingeschränkt (z.B. fehlen Formel-, Abbildungs- und Tabellennummerierungen) und möglicherweise unvollständig oder vom Original abweichend. Die originale, vollständige PDF-Datei des Preprints können Sie hier aufrufen.

Der Forschungsbericht 2011 der Hochschule Merseburg, in dem dieser Artikel abgedruckt ist, erschien am 10. November 2011.

Abschrift des Preprint, eingereicht 2011/06/23
Forschungsbericht 2011 Hochschule Merseburg (FH)

---

Wie weit ist es von Berlin bis Tokio?
Entfernungsberechnung mit Quaternionen und Geodäten.

B.Eng. René Schwarz
Prof. Dr. rer. nat. Hartmut Kröner

Hochschule Merseburg (FH), Fachbereich Informatik und Kommunikationssysteme, Geusaer Str. 88, DE-06217 Merseburg

---

Zusammenfassung

Die Anwendungen von Entfernungsberechnungen zwischen zwei Orten auf der Erde sind in der heutigen Zeit vielfältig. Angefangen von Entfernungsberechnungen in der Flugzeug- und Schiffsnavigation über komplexe Geografische Informationssysteme bis hin zur GPS-gestützten Routenführung von Automobilen durch Navigationsgeräte haben alle eines gemeinsam: Zur Berechnung dieser Entfernungen ist eine mathematische Grundlage notwendig.

Die Tatsache, dass die Erde durch ihre Eigendrehung keine Kugel, sondern ein abgeplatteter Rotationsellipsoid ist, macht diese Art von Berechnungen nicht trivial. Dieser Aufsatz stellt zwei verschiedene Lösungsansätze für diese Berechnungen vor und vergleicht die Ergebnisse mit den bereits bestehenden Verfahren.

Keywords: Christoffelsymbole, Dreibein, Differentialgleichungen, Einsteinsche Summenkonvention, Entfernungsberechnung, Erde, Flächenkurven, Fundamentalgrößen, Geodäten, Krümmung, Kugelparametrisierung, Quaternionen, Rotationen, Tangentialebene

Ausgangssituation und theoretische Grundlagen

Die Berechnung der Entfernung zwischen zwei Punkten auf der Erdoberfläche ist nicht trivial, denn die Erde ist keine perfekte Kugel. Tatsächlich hat die Erde, bedingt durch ihre Eigenrotation, die Gestalt eines abgeflachten Rotationsellipsoiden. Um die Position der betrachteten Punkte beschreiben zu können, muss zunächst eine geeignete Parametrisierung dieser Oberfläche erarbeitet werden.

Einstweilen wird daher eine Parametrisierung über die vereinfachende Annahme einer Kugelform hergeleitet und später auf das Modell eines abgeflachten Rotationsellipsoiden überführt.

Parametrisierung der Erde als Kugel

Der Sinn und Zweck der Kugelparametrisierung besteht darin, explizite Zusammenhänge für die $x$-, $y$- und $z$-Koordinaten einer Kugel zu erhalten. Die Grundannahme besteht in einer Kugel mit einem gegebenen Radius $r$, deren Mittelpunkt im Koordinatenursprung $(0,0,0)^\mathrm{T}$ liegt. Alle zu betrachtenden Punkte liegen auf der Kugeloberfläche; Höhenunterschiede auf der Kugeloberfläche werden vernachlässigt (keine topografische Modellierung).

Jeder Punkt $\tilde{\mathbf{P}}_i$ auf der Kugeloberfläche lässt sich nun durch zwei Winkel $\vartheta_i$ und $\varphi_i$ beschreiben: \begin{gather} \tilde{\mathbf{P}}_i (\vartheta_i,\varphi_i) = \begin{pmatrix} \tilde{P}_x(\vartheta_i,\varphi_i) \\ \tilde{P}_y(\vartheta_i,\varphi_i) \\ \tilde{P}_z(\vartheta_i) \end{pmatrix} = \begin{pmatrix} r \sin \vartheta_i \cos \varphi_i \\ r \sin \vartheta_i \sin \varphi_i \\ r \cos \vartheta_i \end{pmatrix} \\ \text{mit } r = \text{const.}, \vartheta_i \in [0,\pi], \varphi_i \in [0,2\pi[. \notag \end{gather}

Gradnetz der Erde

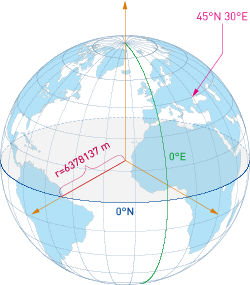
Zur Anwendung dieser Parametrisierung auf das Gradnetz der Erde ist eine Winkelanpassung notwendig, denn das Gradnetz der Erde läuft von $180^\circ$ W bis $180^\circ$ E bzw. $90^\circ$ N bis $90^\circ$ S (vgl. nebenstehende Abb.). Bei dieser Gelegenheit wird der bislang noch nicht definierte Radius $r$ mit dem Erdradius $r_{\earth}$ aus dem WGS84-Referenzellipsoiden belegt.

Dadurch entsteht nun die endgültige Parametrisierung für einen Punkt $\hat{\mathbf{P}}_i$ auf der als Kugel angenommenen Erde mit \begin{gather} \begin{split} \hat{\mathbf{P}}_i (\vartheta_i,\varphi_i) &= \begin{pmatrix} \hat{P}_x(\vartheta_i,\varphi_i) \\ \hat{P}_y(\vartheta_i,\varphi_i) \\ \hat{P}_z(\vartheta_i) \end{pmatrix}\\ &= \begin{pmatrix} r_{\earth} \sin \left( \frac{\pi}{2} - \vartheta_i \right) \cos \varphi_i \\ r_{\earth} \sin \left( \frac{\pi}{2} - \vartheta_i \right) \sin \varphi_i \\ r_{\earth} \cos \left( \frac{\pi}{2} - \vartheta_i \right) \end{pmatrix} \end{split} \\ \text{mit } r_{\earth} = 6\,378\,137\,\text{m}, \vartheta_i \in \left[-\frac{\pi}{2},\frac{\pi}{2}\right], \varphi_i \in \, ]-\pi,\pi]. \notag \end{gather}

Die Berechnung der Distanz zwischen zwei Punkten auf der Kugeloberfläche ist unter Annahme der Kugelgestalt sehr einfach zu realisieren, da es sich bei der kürzesten Verbindung beider Punkte immer um ein Bogensegment eines Kreises mit Radius $r_{\earth}$ handelt. Der Winkel $\varepsilon$ zwischen den beiden Ortsvektoren der Punkte definiert das gesuchte Kreisbogensegment, dessen Länge $d$ dann über \begin{equation} d(\varepsilon) = \frac{\pi \cdot r_{\earth}}{180^\circ} \cdot \varepsilon \end{equation} ermittelt werden kann.

Überführung in einen Rotationsellipsoiden

Durch die Einführung eines »stauchenden« Faktors $f$ in der $z$-Koordinate ist die Überführung in einen abgeplatteten Rotationsellipsoiden nun einfach. Der Stauchungsfaktor $f_{\earth}$ entspricht dabei der Abplattung nach WGS84, die das Verhältnis von kleiner zu großer Halbachse des Erd-Rotationsellipsoiden beschreibt.

Somit kann ein Punkt $\mathbf{P}_i$ auf dem Rotationsellipsoiden der Erde durch \begin{gather} \begin{split} \mathbf{P}_i (\vartheta_i,\varphi_i) &= \begin{pmatrix} P_x(\vartheta_i,\varphi_i) \\ P_y(\vartheta_i,\varphi_i) \\ P_z(\vartheta_i) \end{pmatrix}\\ &= \begin{pmatrix} r_{\earth} \sin \left( \frac{\pi}{2} - \vartheta_i \right) \cos \varphi_i \\ r_{\earth} \sin \left( \frac{\pi}{2} - \vartheta_i \right) \sin \varphi_i \\ r_{\earth} f_{\earth} \cos \left( \frac{\pi}{2} - \vartheta_i \right) \end{pmatrix} \end{split} \\ \text{mit } r_{\earth} = 6\,378\,137\,\text{m}, f_{\earth} = 1 - \frac{1}{298.257\,223\,563}, \notag \\ \vartheta_i \in \left[-\frac{\pi}{2},\frac{\pi}{2}\right], \varphi_i \in \, ]-\pi,\pi] \notag \end{gather} beschrieben werden.

Die Berechnung der Distanz zwischen beiden Punkten entlang der Oberfläche des Rotationsellipsoiden ist nun nicht mehr ohne Weiteres möglich.

Entfernungsberechnung mit Quaternionen

Ansatz

Gegeben seien zwei Punkte $\mathbf{P}_1$ und $\mathbf{P}_2$ auf dem Erdellipsoiden. Der Ansatz des erarbeiteten Verfahrens besteht nun darin, den Ellipsoiden derart zu transformieren, dass $\mathbf{P}_1$ auf der Abszisse liegt und zudem beide Punkte in der $x$-$y$-Ebene ($z=0$) liegen. Anschließend wird die parametrisierte Schnittgleichung der $x$-$y$-Ebene mit dem transformierten Erdellipsoiden ermittelt. Anhand dieser Kurve lässt sich nun die Entfernung über die Bogenlänge ermitteln; als Ergebnis ergibt sich damit die Distanz zwischen beiden Punkten.

Zur schrittweisen Transformation (Rotation) des Rotationsellipsoiden werden Quaternionen verwendet, da sie gegenüber Rotationsmatrizen einige Vorzüge aufweisen:

• kleinerer (numerischer) Rechenaufwand bei verketteten Vektoroperationen
• kompakte Struktur: Quaternionen können mit weniger Speicheraufwand abgelegt werden (4 Elemente, Rotationsmatrix: 9 Elemente)
• Problem des sog. Gimbal Lock, der Verlust eines Freiheitsgrades, wird verhindert

Aufgrund dieser Vorzüge werden Quaternionen häufig in der Luft- und Raumfahrttechnik zur Lageregelung verwendet.

Kurzeinführung in die Quaternionen-Theorie

Quaternionen erweitern die komplexen Zahlen um zwei weitere Dimensionen; es handelt sich somit um hyperkomplexe Zahlen (4-dimensional). Die Struktur ähnelt dabei der komplexer Zahlen: Es existieren ein Realteil und drei Imaginärteile mit den imaginären Einheiten $\ii$, $\jj$ und $\kk$. Ein Quaternion $q$ kann ausführlich mit \begin{equation} q \in \mathbb{H}, \quad q = x_0 + \ii x_1 + \jj x_2 + \kk x_3 \end{equation} oder in Kurzschreibweise \begin{equation} q = \left[ x_0, \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} \right] \end{equation} geschrieben werden. Dabei ist $x_0$ der Realteil und der Vektor $(x_1,x_2,x_3)^\mathrm{T}$ der 3-dimensionale Imaginärteil.

Eine Koordinate $(x,y,z)^\mathrm{T}$ im $\mathbb{R}^3$ kann als Quaternion mit Realteil $0$ und dem Koordinatentripel $(x,y,z)^\mathrm{T}$ als Imaginärteil ausgedrückt werden: \begin{gather} \mathbf{P} = \begin{pmatrix} x \\ y \\ z \end{pmatrix} \Rightarrow P = \left[ 0, \begin{pmatrix} x \\ y \\ z \end{pmatrix} \right] \\ \notag \text{mit } \mathbf{P} \in \mathbb{R}^3, P \in \mathbb{H} \end{gather}

Rotationen sind mit einem Rotationsquaternion \begin{equation} q_R(\alpha, \mathbf{u}) = \left[ \cos \frac{\alpha}{2}, \sin \frac{\alpha}{2} \cdot \mathbf{u} \right] \end{equation} möglich. Dabei ist $\alpha$ der Rotationswinkel, $\mathbf{u}$ die auf $1$ normierte Rotationsachse ($\mathbf{u} \in \mathbb{R}^3, \| \mathbf{u} \| = 1$). Ein gedrehter Punkt $\mathbf{P}^\star$ entsteht nun durch Multiplikation des Rotationsquaternions $q_R$ mit dem Quaternion $P$ des Ursprungspunktes $\mathbf{P}$ und dem hyperkomplex konjugierten Rotationsquaternion $\overline{q_R}$: \begin{equation} P^\star = [0, \mathbf{P}^\star ] = q_R(\alpha, \mathbf{u}) \cdot [0, \mathbf{P} ] \cdot \overline{q_R}(\alpha, \mathbf{u}) \end{equation}

Verfahren zur Entfernungsberechnung

Beschreibung der Verfahrensschritte

Im ersten Verfahrensschritt wird der Rotationsellipsoid (Gleichung für $\mathbf{P}_i (\vartheta_i,\varphi_i)$) derart rotiert, dass der Punkt $\mathbf{P}_1$ mit $(\vartheta_1, \varphi_1)$ auf der $x$-$z$-Ebene liegt. Dazu ist eine Drehung um $\alpha_1 = - \varphi_1$ um die Applikate notwendig. Es entsteht ein gedrehter Rotationsellipsoid \begin{gather} \Prefix^{(1)}{P} = [0, \Prefix^{(1)}{\mathbf{P}}] = q_R(\alpha_1, \mathbf{u}_1) \cdot [0, \mathbf{P}] \cdot \overline{q_R}(\alpha_1, \mathbf{u}_1) \\ \notag \text{mit } \alpha_1 = -\varphi_1, \ \mathbf{u}_1 = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}, \\ \notag \Prefix^{(1)}{\mathbf{P}} \xlongequal{\text{def.}} \begin{pmatrix} \Prefix^{(1)}{P}_x(\vartheta, \varphi, \ldots) \\ \Prefix^{(1)}{P}_y(\vartheta, \varphi, \ldots) \\ \Prefix^{(1)}{P}_z(\vartheta, \varphi, \ldots) \end{pmatrix}. \end{gather}

Analog zum ersten Verfahrensschritt wird der Ellipsoid nun um die Ordinate derart gedreht, dass $\mathbf{P}_1$ auf die Abszisse ausgerichtet wird: \begin{gather} \Prefix^{(2)}{P} = q_R(\alpha_2, \mathbf{u}_2) \cdot \Prefix^{(1)}{P} \cdot \overline{q_R}(\alpha_2, \mathbf{u}_2) \\ \notag \text{mit } \alpha_2 = \arctan \left( \frac{\Prefix^{(1)}{P}_z(\vartheta = \vartheta_1, \varphi = \varphi_1, \ldots)}{\Prefix^{(1)}{P}_x(\vartheta = \vartheta_1, \varphi = \varphi_1, \ldots)} \right), \\ \notag \mathbf{u}_2 = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}, \ \Prefix^{(2)}{\mathbf{P}} \xlongequal{\text{def.}} \begin{pmatrix} \Prefix^{(2)}{P}_x(\vartheta, \varphi, \ldots) \\ \Prefix^{(2)}{P}_y(\vartheta, \varphi, \ldots) \\ \Prefix^{(2)}{P}_z(\vartheta, \varphi, \ldots) \end{pmatrix}. \end{gather}

Im letzten Transformationsschritt wird $\Prefix^{(2)}{\mathbf{P}}$ so gedreht, dass der Punkt $\mathbf{P}_2$ auf der $x$-$y$-Ebene liegt: \begin{gather} \Prefix^{(3)}{P} = q_R(\alpha_3, \mathbf{u}_3) \cdot \Prefix^{(2)}{P} \cdot \overline{q_R}(\alpha_3, \mathbf{u}_3) \\ \notag \text{mit } \alpha_3 = - \arctan \left( \frac{\Prefix^{(2)}{P}_z(\vartheta = \vartheta_2, \varphi = \varphi_2, \ldots)}{\Prefix^{(2)}{P}_y(\vartheta = \vartheta_2, \varphi = \varphi_2, \ldots)} \right), \\ \notag \mathbf{u}_3 = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}, \ \Prefix^{(3)}{\mathbf{P}} \xlongequal{\text{def.}} \begin{pmatrix} \Prefix^{(3)}{P}_x(\vartheta, \varphi, \ldots) \\ \Prefix^{(3)}{P}_y(\vartheta, \varphi, \ldots) \\ \Prefix^{(3)}{P}_z(\vartheta, \varphi, \ldots) \end{pmatrix}. \end{gather}

Mit $\Prefix^{(3)}{\mathbf{P}}$ steht nun eine Parametergleichung für die transformierte Erde zur Verfügung. Beide Punkte $\Prefix^{(3)}{\mathbf{P}}_1$ bzw. $\Prefix^{(3)}{\mathbf{P}}_2$ im transformierten Koordinatensystem liegen nun in der $x$-$y$-Ebene; die $z$-Komponente ist jeweils Null.

Herleitung des Lösungswegs

Die Bogenlänge zwischen zwei Punkten auf einer ebenen, rektifizierbaren Kurve mit dem Parameter $t \mapsto \left( x(t), y(t) \right)^\mathrm{T}$ kann allgemein mit \begin{equation} \alpha \leq t \leq \beta: \ \int \limits_{\alpha}^{\beta} \sqrt{\dot{x}(t)^2 + \dot{y}(t)^2} \, \dd t \end{equation} ermittelt werden. Hierbei hängt die vorhandene Parametergleichung $\Prefix^{(3)}{\mathbf{P}}$ jedoch von zwei Parametern $\vartheta$ und $\varphi$ ab. Eine Einschränkung auf einen Parameter ist daher notwendig, so dass eine zwei-dimensionale Parametergleichung \begin{equation} \Prefix^{(4)}{\mathbf{P}} = \begin{pmatrix} \Prefix^{(4)}{P}_x (\varphi) \\ \Prefix^{(4)}{P}_y (\varphi) \end{pmatrix} = \begin{pmatrix} \Prefix^{(3)}{P}_x \left(\vartheta(\varphi), \varphi \right) \\ \Prefix^{(3)}{P}_y \left(\vartheta(\varphi), \varphi \right) \end{pmatrix} \end{equation} entsteht. Da für das Verfahren lediglich der Schnitt durch $z=0$ relevant ist, erhält man durch Lösung von $\Prefix^{(3)}{P}_z(\ldots) \stackrel{!}= 0$ einen Zusammenhang beider Parameter: $\vartheta(\varphi) = \ldots$

Schließlich ergibt sich der Abstand beider Punkte durch Integration von \begin{equation} \int \limits_{\varphi_1}^{\varphi_2} \sqrt{\left( \frac{\dd}{\dd \varphi} \ \Prefix^{(4)}{P}_x(\varphi) \right)^2 + \left( \frac{\dd}{\dd \varphi} \ \Prefix^{(4)}{P}_y(\varphi) \right)^2} \, \dd \varphi. \end{equation}

Entfernungsberechnung mit Geodäten

Einführung

Die Krümmung $k$ eines Kreises mit Radius $R$ ist $k=\frac{1}{R}$. Allgemein heißt $\gamma: \mathbb{R} \to \mathbb{R}^3$, $t \to \gamma(t)$ zulässige Parametrisierung einer Kurve, wenn die Abbildung dreimal stetig differenzierbar und $\gamma'(t) \neq 0$ (ein ${}^\prime$ meint die erste Ableitung nach dem Parameter), d.h. genau dann, wenn die Jacobische maximalen Rang hat. Für rektifizierbare Kurven wählt man als Parameter die Bogenlänge $s$ ("`natürlicher Parameter"') und die Krümmung $k$ ist definiert als $k := \| \gamma^{\prime\prime}(s) \|$. (Hier ist $\|\ldots\|$ die Euklidische Norm).

Normalkrümmung einer Flächenkurve: Sei $(P_1(u^1,u^2),P_2(u^1,u^2),\mathbf{n}(u^1,u^2))$ das begleitende Dreibein einer Fläche mit zulässiger Parametrisierung $P: \mathbb{R}^2 \to \mathbb{R}^3$, $(u^1,u^2) \to P(u^1,u^2)$ (d.h. die Abbildung ist dreimal stetig differenzierbar und die Jacobische hat maximalen Rang). Hier ist $P_1(u^1,u^2) := \frac{\partial P}{\partial u^1}$, $P_2(u^1,u^2) := \frac{\partial P}{\partial u^2}$, $\mathbf{n}$ sei der Normalenvektor. $P_1$ und $P_2$ sollen nicht parallel sein.

Die Normalkrümmung $k_n$ einer Flächenkurve ist die Komponente von $\gamma^{\prime\prime}$ bezüglich des Normalenvektors. Die Komponente von $\gamma^{\prime\prime}$ bezüglich der Tangentialebene heißt geodätische Krümmung $k_g$. Insgesamt gilt \begin{equation} \gamma^{\prime\prime} = k_n \mathbf{n} + k_g \mathbf{e} \end{equation} und \begin{equation} k^2 = k_n^2 + k_g^2 \end{equation} mit dem Einheitsvektor $\mathbf{e}$ in der Tangentialebene.

Fundamentaltensor, Bogenlänge, Geodäten

Geodäten sind »geradeste« Flächenkurven, auf ihnen liegen Kurven kürzester Entfernung. Die Krümmung wird auf Geodäten minimal. Das ist genau dann der Fall, wenn die geodätische Krümmung verschwindet und $k = k_n$ wird.

Beispiel 1

Ein Kreissegment mit Radius $R_1$ verbindet zwei Punkte auf einer Kugel mit Radius $R > R_1$. Längs des Kreissegments »fährt« man einen Umweg.

Das Differential der Bogenlänge $\dd s$ einer Flächenkurve genügt der Riemannschen Formel \begin{equation} \dd s^2 = g_{ik} \dd u^i \dd u^k \end{equation} (Summenkonvention) mit $g_{ik} := \langle P_i, P_k \rangle$; $(g_{ik})$ ist der metrische Tensor.

Die Differentialgleichungen der Geodäten lauten für $u^j = u^j(s)$ \begin{equation} u^{r\prime\prime} + \Gamma^r_{ik} u^{i\prime} u^{k\prime} = 0 \end{equation} mit $r \in \{1,2\}$ und den Christoffelsymbolen $\Gamma^r_{ik}$, wobei $\Gamma^r_{ik} = \Gamma^r_{ki}$.

Genauer ist \begin{equation} \begin{split} \Gamma^1_{ij} =& \frac{1}{2} g^{11} (g_{j1,i} + g_{i1,j} - g_{ij,1}) \\ &+ \frac{1}{2} g^{12} (g_{j2,i} + g_{i2,j} - g_{ij,2}) \end{split} \end{equation} für $r = 1$ und $(g^{rk}) = (g_{rk})^{-1}$ sowie \begin{equation} \begin{split} \Gamma^2_{ij} =& \frac{1}{2} g^{21} (g_{j1,i} + g_{i1,j} - g_{ij,1}) \\ &+ \frac{1}{2} g^{22} (g_{j2,i} + g_{i2,j} - g_{ij,2}) \end{split} \end{equation} für $r = 2$.

Beispiel 2

Bei einer Ebene ist $\Gamma^r_{ik} = 0$. Die Integration von $u^{r\prime\prime} = 0$ führt auf lineare Funktionen, d.h. auf der Ebene sind die Geodäten die Geraden.

Beispiel 3

Für Kugelkoordinaten nehmen wir $u^1 := \vartheta$ (Parameter), $u^2 := \varphi$ und betrachten $u^2 = \text{const.}$ Für $r=1$ erhalten wir $u^{1\prime\prime} = 0$, $u^{2\prime} = 0$ und $0 = 0$. Für $r = 2$ wird ebenfalls alles null. Großkreise (durch Nord- und Südpol) sind also Geodäten.

Um Entfernungen auf gekrümmten Flächen zu berechnen, benötigt man noch Randbedingungen und bekommt ein nichtlineares Randwertproblem.

Differentialgleichungssystem 1. Ordnung für die Geodäten

Ein System erster Ordnung mit vier Differentialgleichungen erhält man aus den Differentialgleichungen zweiter Ordnung wie folgt: \begin{equation} \begin{split} &v' = x(t), \ x' = - 2\Gamma^2_{12} x(t) y(t), \ u' = y(t), \\ &y' = - \Gamma^1_{11} y(t)^2 - \Gamma^1_{22} x(t)^2 \end{split} \end{equation} mit $u := u^1$, $v := u^2$ bei $\Gamma^2_{11} = \Gamma^2_{22} = 0$, $\Gamma^1_{12} = 0$ und vier Randbedingungen (nur für $u$ und $v$, nicht für $x$ und $y$!) \begin{equation} u(0) = \vartheta_1, \ u(1) = \vartheta_2, \ v(0) = \varphi_1, \ v(1) = \varphi_2. \end{equation}

Ergebnisdiskussion

Die Proberechnungen mit Mathematica (Ergebnisse siehe Tabelle) zeigen, dass die Ergebnisse der beiden hier neu vorgestellten Verfahren gegenüber dem etablierten Verfahren von Jean Meeus (siehe Literaturverzeichnis) geringfügig abweichen, während die Quaternionen- und Geodätenmethode untereinander lediglich Abweichungen im Meter-Bereich aufweisen.

Mit unterschiedlichen Verfahren errechnete Entfernungen zwischen den angegebenen Orten. Alle Angaben in $\text{km}$.

	Meeus	Quaternionen	Geodäten
Berlin ↔ Tokio	$8.941{,}21$	$8.924{,}69$	$8.924{,}67$
Paris ↔ Washington	$6.181{,}63$	$6.171{,}22$	$6.171{,}22$
Shanghai ↔ Istanbul	$8.003{,}13$	$7.992{,}73$	$7.992{,}72$
Lagos ↔ Buenos Aires	$7.906{,}35$	$7.911{,}68$	$7.911{,}68$
Kapstadt ↔ Bogota	$10.527{,}00$	$10.528{,}40$	$10.528{,}40$

Es bleibt zu klären, ob die hier vorgestellten Verfahren somit genauer sind, als das derzeit verwendete Verfahren von Meeus.

Literatur

• Formella, A.; Fellner, D.: Rotation mit Quaternionen. Universität Braunschweig. Online: http://trevinca.ei.uvigo.es/~formella/doc/ig04/node97.html. 2004/2005. Retrieved 2011/06/22.
• Gauß, Carl F.: Disquisitiones Generales Circa Superficies Curvas. 1827. – Deutsche Übersetzung von Wangerin, A. 1889.
• Klotzek, Benno: Einführung in die Differentialgeometrie I. Deutscher Verlag der Wissenschaften, Berlin, 1981.
• Klotzek, Benno: Einführung in die Differentialgeometrie II. Deutscher Verlag der Wissenschaften, Berlin, 1983. ISBN 9783326004259.
• Kuipers, Jack B.: Quaternions and Rotation Sequences: A Primer with Applications to Orbits, Aerospace and Virtual Reality. 5th printing. Princeton University Press, Princeton, New Jersey, USA, 2002. ISBN 0691102988.
• Meeus, Jean: Astronomical Algorithms. 2nd edition. Willmann-Bell, Richmond, Virginia, USA, 2009. ISBN 9780943396613.

Dieser Artikel ist urheberrechtlich geschützt und steht – im Gegensatz zu den meisten anderen Inhalten meiner Internetseiten – nicht unter der Creative Commons CC-BY-SA-NC Lizenz. Die Weiterverwendung des Artikels oder seiner einzelnen Bestandteile ist ohne schriftliche Genehmigung der Autoren untersagt.