Neuer Artikel: Wie weit ist es von Berlin bis Tokio? Entfernungsberechnung mit Quaternionen und Geodäten
Für den Forschungsbericht 2011 der Hochschule Merseburg (FH) wurde in der vergangenen Woche der Artikel »Wie weit ist es von Berlin bis Tokio? Entfernungsberechnung mit Quaternionen und Geodäten.« eingereicht.
Dieser Artikel beschreibt die Resultate einer gemeinschaftlichen Forschungsarbeit mit Herrn Prof. Dr. rer. nat. Hartmut Kröner, Professor für Ingenieurmathematik und Numerische Methoden an der Hochschule Merseburg (FH), bezüglich Entfernungsberechnungen zwischen zwei Punkten auf der Erde mit zwei neuen, voneinander unterschiedlichen Verfahren. Die Ergebnisse der Proberechnungen werden mit denen eines etablierten Verfahrens verglichen.
Der Forschungsbericht 2011 erscheint am 10. November 2011. Der Preprint des Artikels ist hier vorab einsehbar. Ich danke Herrn Prof. Kröner vielmals für die konstruktive und erquickliche Zusammenarbeit in diesem Projekt und hoffe auf viele weitere gemeinsame, spannende Projekte.
Zusammenfassung
Die Anwendungen von Entfernungsberechnungen zwischen zwei Orten auf der Erde sind in der heutigen Zeit vielfältig. Angefangen von Entfernungsberechnungen in der Flugzeug- und Schiffsnavigation über komplexe Geografische Informationssysteme bis hin zur GPS-gestützten Routenführung von Automobilen durch Navigationsgeräte haben alle eines gemeinsam: Zur Berechnung dieser Entfernungen ist eine mathematische Grundlage notwendig.
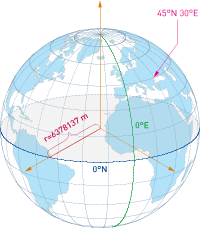
Die Tatsache, dass die Erde durch ihre Eigendrehung keine Kugel, sondern ein abgeplatteter Rotationsellipsoid ist, macht diese Art von Berechnungen nicht trivial. Dieser Aufsatz stellt zwei verschiedene Lösungsansätze für diese Berechnungen vor und vergleicht die Ergebnisse mit den bereits bestehenden Verfahren.
Keywords: Christoffelsymbole, Dreibein, Differentialgleichungen, Einsteinsche Summenkonvention, Entfernungsberechnung, Erde, Flächenkurven, Fundamentalgrößen, Geodäten, Krümmung, Kugelparametrisierung, Quaternionen, Rotationen, Tangentialebene







 Science
Science